-
目次
- 対角線分割法の公式
- 四角形ならなんでも適用できる
- 透視図法の分割目盛り時代の到来
- 垂直方向と水平方向の奥行きは比例の関係
- 対角線分割法で風景画を描く、つもりだった
- 奇数分割
- R点法
- 透視図法の原理は対角線分割法の集積
- 足線法
- M点法
- D点法
- にぼし遠近法
- 対角線分割法、実用化の兆し
- 真理の扉の向こうにある「真・対角線分割法」
今回の記事は以前から独自開発していた対角線分割法のとりあえずの完全版リリース報告です。半年前に透視図法の基本原理「対角線分割法」誕生の軌跡 〜3次元を2次元に変換する仕組み〜の記事でキッカケを掴んでから実用性の模索をしていたのがやっと形になりました。
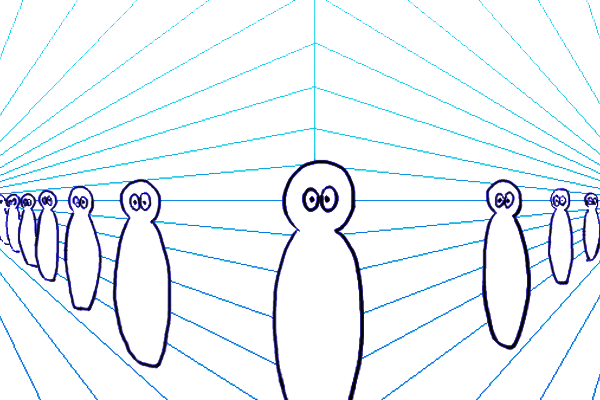
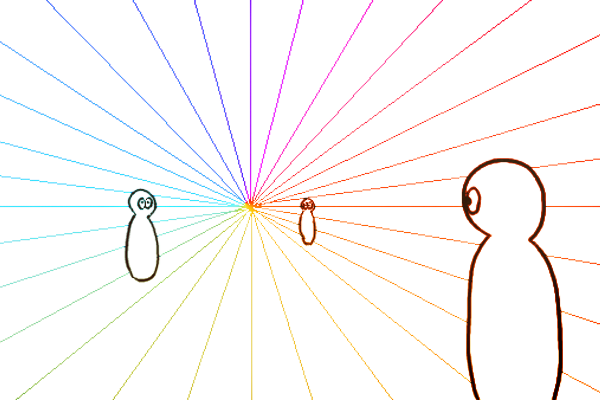
本来の透視図法は、被写体のシルエットを透明板にプロットしていくという原始的な作図方法です。透視図法に目線の高さ(アイレベル)という概念を導入して作図手法として理論化した足線法は、様々な4つの点の組み合わせで対角線の交点を作図することで3次元と2次元を変換する手法です。平面図と透視図はアングルが違うだけで同じ空間を表しているため、平面図で4つの点を選んで平面的に対角線を作図し、透視図上で対応する4つの点で対角線を作図すれば立体的なアングルから見た対角線となり、その交点はパースにのった奥行きということになります。
今回の記事の後半は、この透視図法の原理の根幹を成す対角線分割法を使って透視図法にまつわる様々な手法の中身が対角線分割法で構成されていることを可視化していく遊びです。最後に対角線分割法で独自の作図手法が発明できるかもしれないことにも触れています。とりあえずは対角線分割法の実用性と、透視図法は対角線分割法の集積であることが伝われば満足です。お絵描きにも応用できる便利な手法として布教したいので、対角線分割法の理論を分かりやすくまとめた決定版として読んで頂ければと思います。
対角線分割法の公式
対角線分割法とは、面(壁・床など)の奥行きを対角線を利用して任意の数で分割する、台形の対角線の性質に基づく手法です。対角線分割法は、数値計算で求める方法と、作図によって求める方法があります。
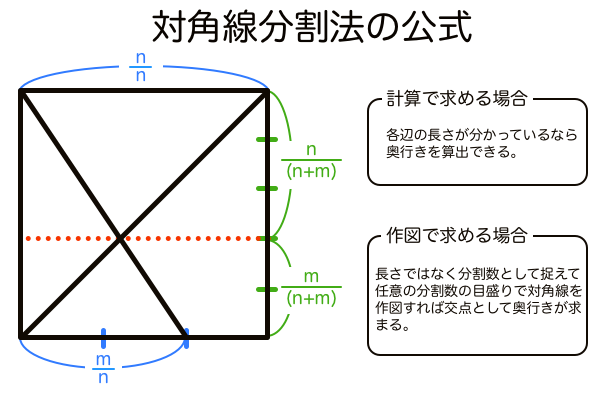
数値計算で求める場合は、すでに作図されている面(壁・床など)の各辺の寸法を定規で測定し、その数値を公式に代入して算出します。
作図で求める場合は、nとmを長さではなく分割数の目盛りとして捉え、作図したい奥行きの長さから逆算してnとmの値を決定します。奥行きは、対角線を作図するときの辺の長さが短い方に近くなります。また、分割数目盛りをいくつにすれば奥行きがいくつになる、ということをある程度暗記しておけば手前の辺を何分割するかを考えるだけで思い通りの奥行きが作図できます。

上図は平面的な正方形を分割する手順です。平面的なら2/5分割したいときそのまま2/5分割すれば済みます。この正方形がパースにのったとき、目分量では正確な2/5分割ができなくなります。ですが平面的であろうとパースにのっていようと、対角線分割法の手順は上図の通りです。四角形であれば適用できます。
四角形ならなんでも適用できる
手前と奥の辺が平行な図形(正方形・長方形・台形・菱形)であれば対角線分割法が適用できます。とくに1点透視図法、2点透視図法では面(壁・床など)は奥行きが縮小されているため全て台形になりますが、実際の建築物は正方形なり長方形なりで構成されているので、対角線分割法によって奥行きの分割数をコントロールして思い通りの位置に窓や柱を作図できます。要は向かい合う一対の辺が平行でさえあれば、辺の長さがどうであれ、互いの距離がどうであれ、対角線で分割できます。
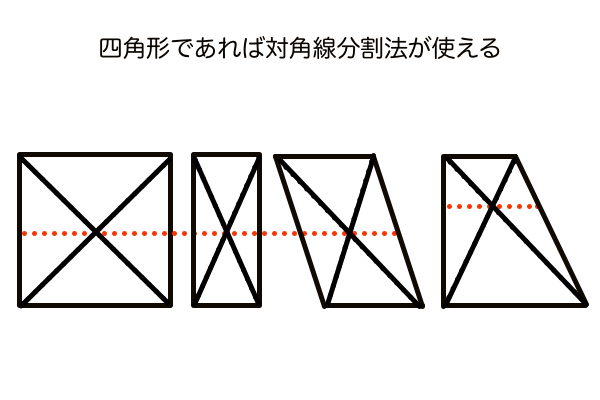
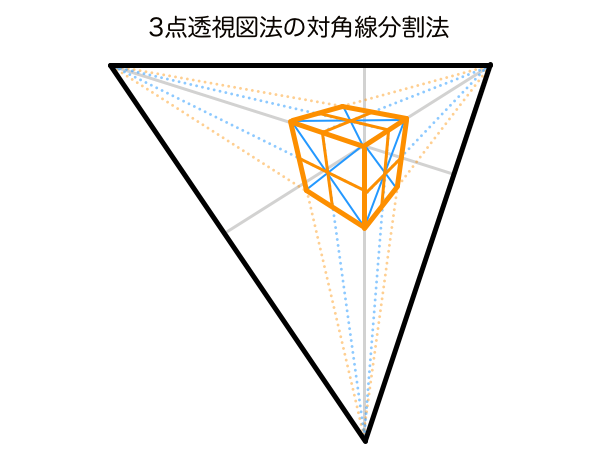
ちなみに手前と奥の辺が並行でなくても分割することはできます。3点透視図法では全方向に奥行きの縮小が生じるので台形にはなりません。しかしパースにのる前が正方形もしくは長方形だったのであれば問題なく対角線分割法の管轄です。歪な四角形に対角線を作図し、消失点の方向へ収束する角度の分割線を作図すればいいだけです。
透視図法の分割目盛り時代の到来
透視図法で描く、と言うと寸分の狂いなく高精度な作図をするものだと思われるかも知れませんが、最近では定規を使わず目分量で作図しても影響が少ない方法もあると分かりました。それが「分割目盛り」です。画面上での「1m」を描けと言われても判断に困りますが、画面上の線の「4分割」なら目分量で描けます。それに平面の四角形に対角線や目盛りを作図しておいて、それをパースにのせるという処理も簡単にできるので用途が広いです。お絵描きに活用するならフリーハンドでパース作画できた方が便利なので、今後はなるべく定規で正確に測定したり、数式で正確に算出したり、という方針はとらないようにしたいですね。すでにある線(立体の辺、画面幅など)を大まかに分割し、それを平面図と透視図で対応させながら位置合わせをすることで奥行きを作図する、という手法が望ましいです。
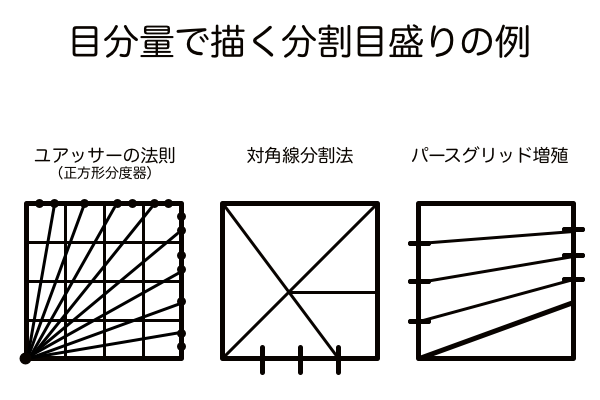
垂直方向と水平方向の奥行きは比例の関係
ここの項目は対角線分割法の原理の一つを数学的に証明したいだけのものです。後述のR点法の補足で少し登場しますが、はっきりいって現段階ではお絵描きにほぼ無関係なので読み飛ばしてください。透視図法オタクは必見です。
対角線分割法の分割線は、基本的にはイメージのしやすいよう上で掲載した公式図のように向かい合う辺と平行方向に作図されます。ところが、面白いことに同じ対角線の交点に垂直方向(公式図と直行する方向)の分割線を描いたとしても、それは対角線の基準になっている片方の線の傾きによって一定の比率が維持されるようになっており、この法則は作図に応用できます。これは数学でよく見る比例グラフだと考えれば簡単に説明がつきます。
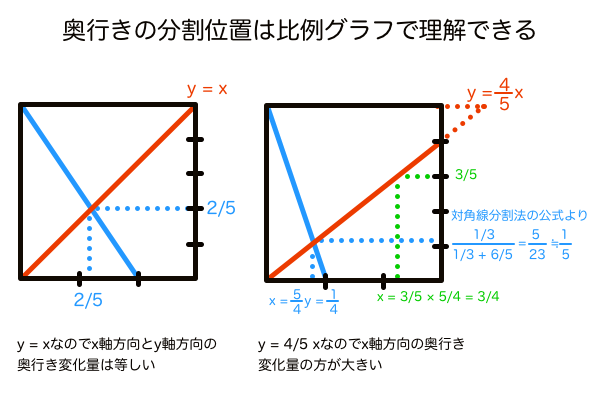
普通の対角線分割法では向かい合う辺と垂直方向(水平面すなわち底面の奥行き)に分割しますが、向かい合う辺と平行方向(垂直面すなわち側面の奥行き)の分割数も同時に求めることができます。このときの透視図上の被写体の面(壁・床など)をグラフの枠に見立て、その面に作図した対角線をグラフ曲線に見立てることで、対角線分割法をパースに乗ったグラフに置き換えて考えることができます。そして対角線分割法の目分量の分割目盛りをグラフのx軸とy軸目盛りに見立て、対角線の角度をグラフの傾き係数aに見立てることで、対角線を片方だけ作図すれば傾き係数aで比率を合わせて同時に側面と底面の分割線も作図できます。
この比例グラフのような性質を活用する場面があるとすれば、例えば建物の壁が見切れていて十分な寸法情報が得られない時、少ない寸法情報から傾きaの直線を描き、その直線上から垂直線(y)と水平線(x)を伸ばして建物の壁の端との交点の寸法がいくつになるかを算出することで寸法情報を連鎖的に増殖させることができる、といったところでしょうか。寸法情報が増えれば対角線分割法で目分量の分割目盛りを利用して任意の分割位置を求めることもできるようになります。ただ、ここまでくると絵を描くという目的を忘れてしまいそうなので、数学に取り憑かれる一種の呪いか何かだと思って取り扱ってください。一応のところ比例グラフの性質は透視図法界のオカルトとして語り継いでおいて、あとで自分自身で怪しい実験をやっていることでしょう。
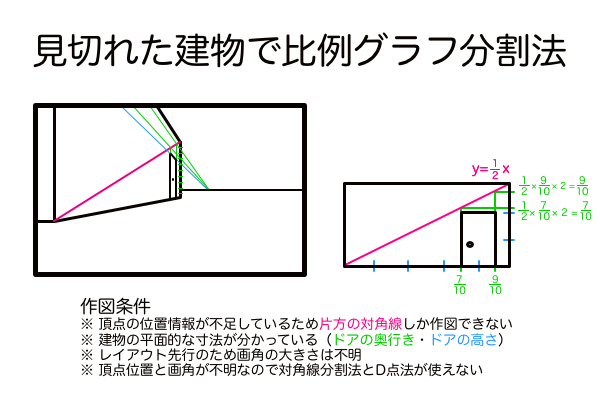
対角線分割法で風景画を描く、つもりだった
とりあえず何か試し描きしてみようといろいろと構図を考えて見ましたが、やはり元々がただの法則である対角線分割法をメインで使う描き方というのを思いつきませんでした。描こうと思えば色々なことができますが、それは他の手法で代替できることがほとんどです。基本的にはD点法、M点法、ユアッサーの法則あたりでパースを取っておいて、建物や立体の表面のディテールの寸法を測定する目的で対角線分割法を使うというのがオススメです。対角線分割法は3DCGのテクスチャマッピングを人力でやる手法だと認識していただいて構わないと思います。
今の所は上で述べた比例グラフ分割法のように、寸法情報を捻出しなくてはいけないシチュエーションが得意と分かっている程度ですが、しばらく試行錯誤を繰り返せば何かしらの使い道が見えてくると思うので一旦保留です。広く応用できる法則なので覚えておくと有利です。
2分割法
ここからは一般的に知られている手法の原理の中身を可視化していく試みです。透視図法で対角線を使うと言えば、奥行きを2分割するものがよく知られています。しかし、この手法だけではどう組み合わせても3の倍数分割と奇数分割ができないのが難点です。
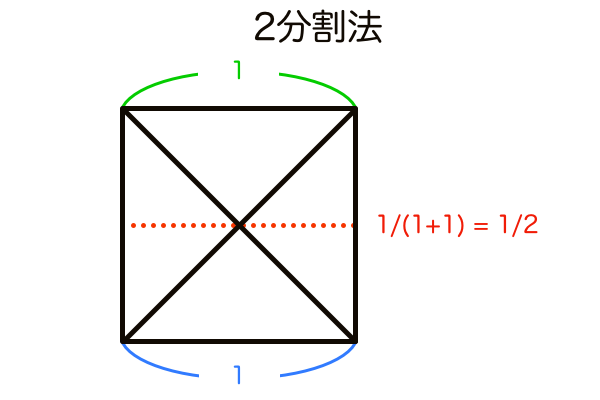
奇数分割
複雑な手順を踏めば3の倍数分割や奇数分割(1/3、1/5、1/6、1/7…)もできます。対角線分割法で奇数分割法の中身がどうなっているのかを可視化してみました。
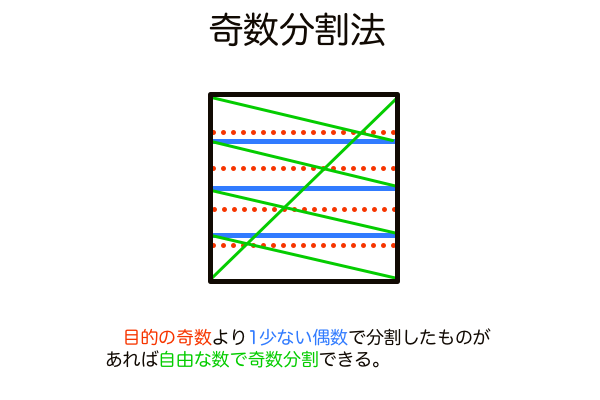
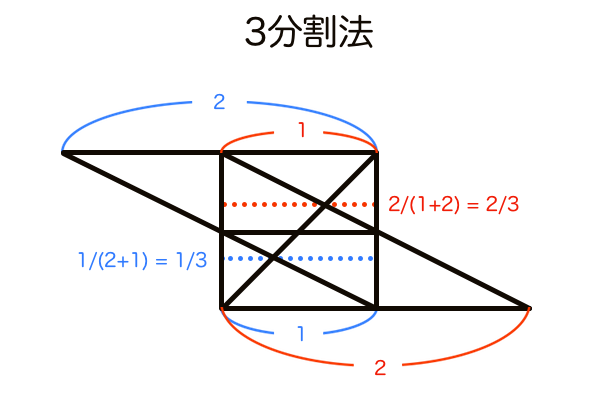
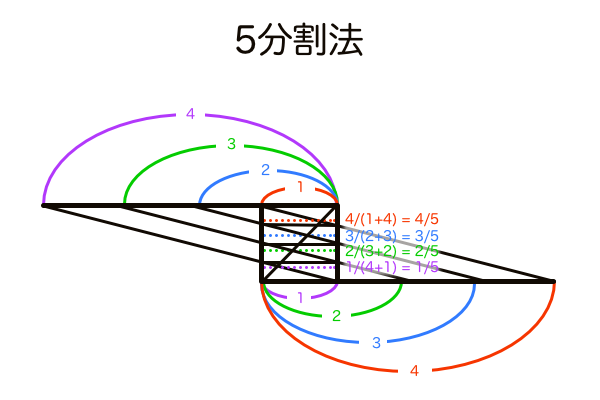
どれだけ分割数が増えようと作図手順は同じです。違う部分といえば、分割したい奇数マイナス1分割するところだけです。

R点法
R点法とは比率点(Ratio Point)を使った作図手法です。以前に奇数分割法から着想を得て対角線分割法を開発する考察ツイートの過程から生まれたもので、一般では奇数分割法を簡略化する代替案として知られており、それに独自に命名しただけのものです。R点法の奥行きを求める手順はM点法とほぼ同じ原理で作られています。相違点を挙げるなら、M点法が立体の平面的な寸法情報から奥行きの全長と分割点の両方を作図できるのに対し、R点法はすでに奥行きの長さが作図された面の分割しかできないところです。ですがそれはM点とR点の機能の違いというだけの話なのであまり気にすることではありません。
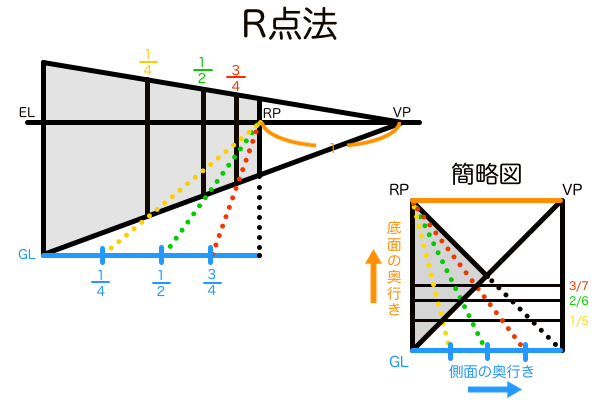
R点法は普通の対角線分割法とは分割する方向が違います。上図の簡略図を見ると公式通りの分割方向、つまり向かい合うオレンジと青の辺と平行方向に分割線を作図しています。ところが作図したかったのは壁の側面の奥行きであって、床の奥行きではありません。ですが、これは上で説明した比例グラフの性質によって側面と底面の奥行きの比率は一定に保たれているため問題ありません。上図のR点法では対角線分割法によって底面の奥行きを求めることで連鎖的に側面(壁)の奥行きを求めているというだけです。
透視図法の原理は対角線分割法の集積
ここまでは2分割法、奇数分割法、R点法といった、すでに作図された面を分割する手法についての説明でした。以降は足線法、M点法、R点法、1/n点法といった、何もない状態から面そのものを作図する手法についての説明と言えます。ただ、既存の手法を対角線分割法で解析したいというだけの遊びなので実用性はありませんが、既存の手法と対角線分割法への理解は深まると思います。理解が深まれば平面図と透視図の対応も脳内イメージで補完できるようになり、最終的には透視図上のみ、つまり画面内だけで作図を完結させられるようにもなると思います。
足線法
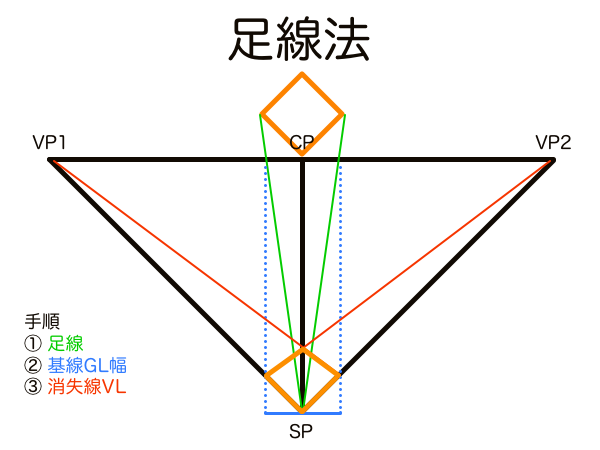
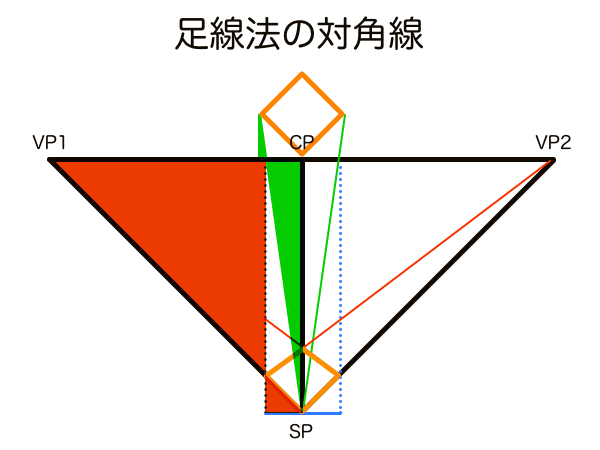
足線法は現実空間で見えているものをそのまま再現した手法なので理屈抜きにして間違いなく正しい手法です。これはとても重要なことなので透視図法を学ぶ上で度々原点回帰することをお勧めします。観測者の立ち位置から地平線までの広大な3次元空間を2次元に落とし込むわけですが、その2次元という概念の権化が透明板です。
足線法における「足線」の基本的な機能は被写体の奥行きの縮小量を測定することです。足線で作図した奥行きが縮小された幅と、VPに向かう線との兼ね合いで奥行きの長さを作図する手法ということです。そして足線法の正式な作図手順も解剖すれば全て対角線分割法で構成されているのが面白いところです。
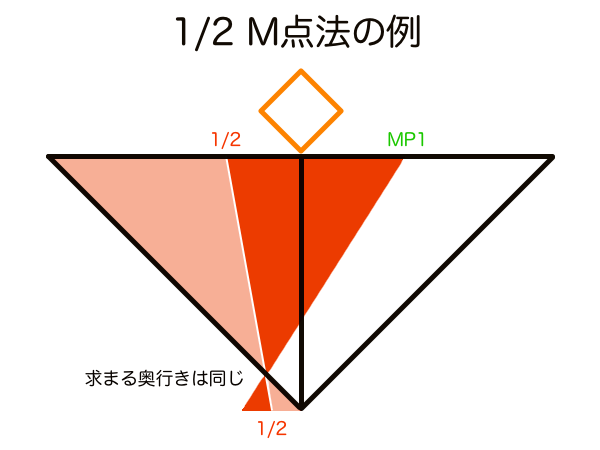
M点法
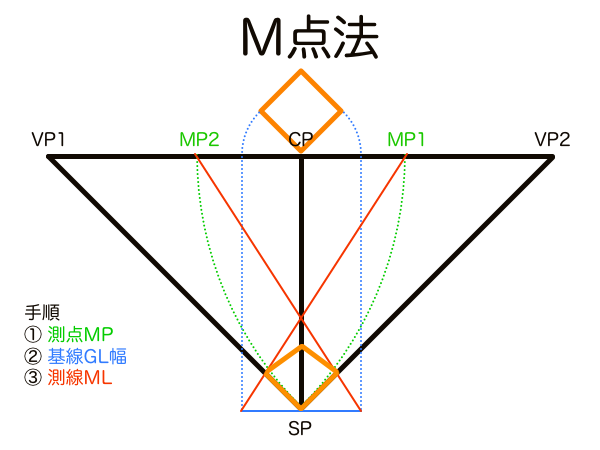
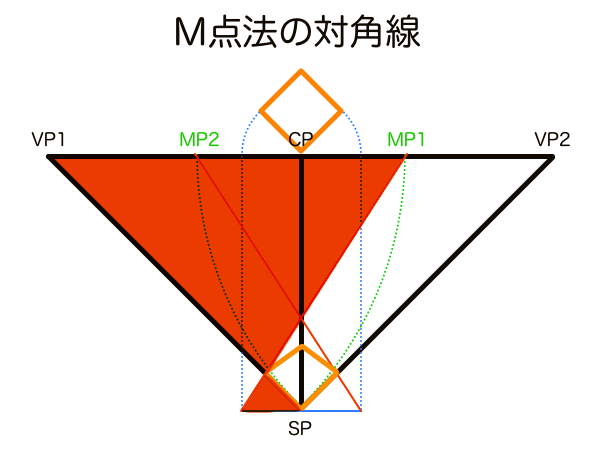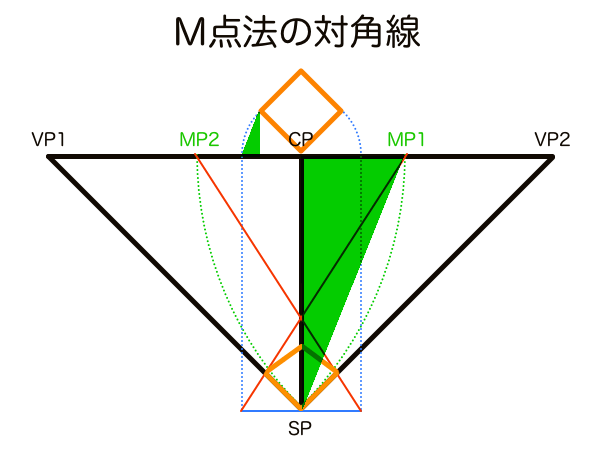
M点法(Majoring Point)は、奥行き方向の寸法の作図を効率化することに特化した手法です。例えば足線法は透視図法をそのまま作図手法に落とし込んだものなので比率変換や幾何学の法則を用いることはせず、作図手順の一番初めに全ての被写体の頂点に足線を作図して奥行きの縮小を測る作業を律儀に行います。奥行きの縮小は目分量では作図できないのでそこでフリーハンドは手詰まりです。一方、M点法はまず奥行きを知りたい頂点の数だけ対応するMPを幾何学の法則を利用して作図しておき、そして作図する位置のGL上に任意の平面的な辺の寸法を描きさえすれば、あとは線を1本作図するだけで完了できます。このMPの機能はまず平面図である1本の直線を作図することで透視図上にある1点(MP)を設定し、「平行線は無限遠で同じ点に収束する」原理を利用して同じ方向すなわち平行に配置された立方体の奥行きを一括して測定するものです。M点法の詳しい原理解説はありそうでなかったM点法の原理解説 〜地平線に隠された秘密〜の記事に載せてあります。
平行な辺は同じMPを流用できるので、どれだけ立体が増えても同じMPに線を引くだけです。ただし立体の向きが異なるなら個別にMPを求める必要があります。とても便利な手法ではありますが、足線法もM点法も作図には画面外のVPやSPを利用する必要があるため画面内だけ作図を完結させることは難しく、あくまで透視図法の原理を活用する方法というだけで、作図手法としてはまだ未完成ということは理解しておいてください。
D点法
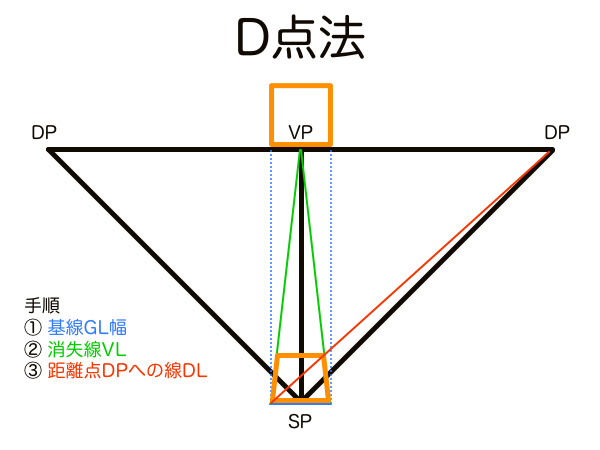
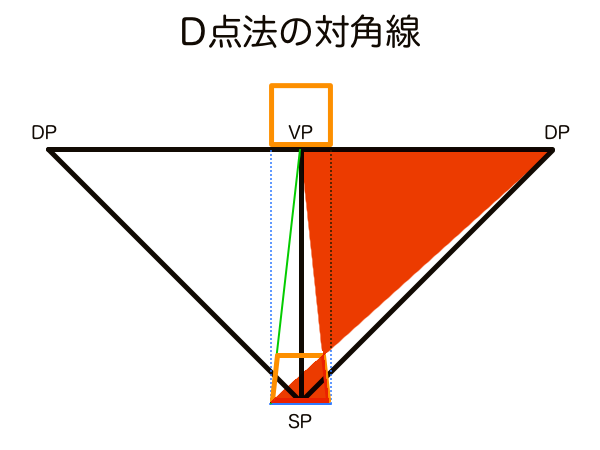
D点法は、正方形を作図するため手法です。1点透視図法の正方形の対角線方向の消失点のことを距離点DP(Distance Point)といい、正方形の奥行きの長さを測定する機能があります。奥行きの長さは左右のDPーDP間距離によってコントロールできるため、1点透視の画角を設定するためにもDPが使われます。初めにDPの位置を決めておけば効率的に正方形を量産できるためグリッド作図の際に活躍します。
ちなみに1点透視のときの正方形の対角線方向の消失点のことを距離点DPと呼び、2点透視のときのそれは対角消失点DVPと個人的に呼んでいます。呼び分けている理由は、2点透視では正方形に方位角が与えられるとVP1-DVP-VP2間距離が複雑に移動しますが、1点透視の正方形は常に正面を向いているため対角線方向の消失点が動くことがなく、作図の基準として使える常駐する点という意味があると考えて区別しているからです。DPは画角90°のとき作図フレームのちょうど両端に位置するため画角を決める基準点にするには最適なので、ユアッサーの法則の画角メーターなどはD点法と目分量の分割目盛りを活用して画角をコントロールしています。
1/n点法
1/n点法は比率変換によって画面内だけで作図を完結させるためのアイデアです。足線法、D点法、M点法、R点法、全ての作図手法において適用させることができます。1/n点法は、向かい合う2つの辺の長さを変えても、長さの比率が変化しなければ対角線の交点の位置は変わらないという、すなわち台形の対角線の性質に基づく手法といえます。そして以前の記事で1/n点法の機能を手軽に使えるように応用して編み出した手法が「対角線分割法」であるとだけ言っておきましょう。
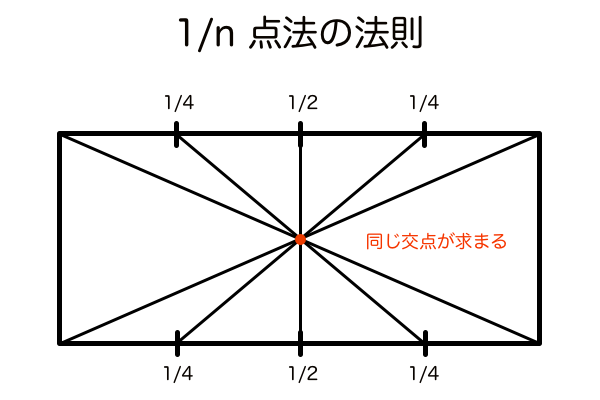
それに1/nというだけあって目分量の分割目盛りで分割することが簡単にできます。もし絵を描いているときに画面内で作図が完結できなさそうなときに、ササッと1/2くらいの点を探してしまえるように習得しておくとかなり応用力が身につきます。透視図法の既存のルールに囚われずに知りたい点を自由気ままに導きたいならオススメの理論です。
にぼし遠近法
イラストや漫画を描かれている
では対角線分割法と相性がいいというのはどういうことか。まず、
ちなみに、カメラが前後に移動するというのは距離が変化しているという考え方をされるかもしれませんが、この場合体感距離は変化しません。赤いさしみさんの動画を見ると、
— 赤井さしみ (@sas_akai) 2017年9月30日
まさに「描いている絵のレンズ感を変える」ことこそがお絵描きパースを学ぶ目的といって良いかもしれません。レンズ感、具体的にいえば画角を考慮せずに絵を描くなら、消失点「的」な点を設定して線を描くだけで完了します。だからこそ画角という概念を理解する努力をするわけですが、
赤いさしみさんの動画ではレンズ感の変化する透視図上の映像しか映っていないので、
出典 お絵描きホーホー論
下のツイートは
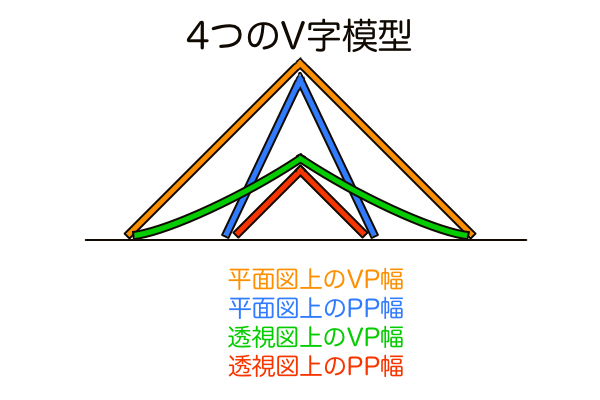
前の記事で考案した「4つのV字模型」でやりたかったことが形にできた。言葉で説明するのでなくいわゆる具象的な説明ができる。画角変化とGL変化による奥行きの変化をリアルタイムで見たかった。画角変化では奥行きの縮小と圧縮があるけど、GL変化では縮小がないことがわかる。https://t.co/WVVco420H2 pic.twitter.com/YPEG0y49cz
— お絵描きホーホー論 (@oekaki_hoho_ron) 2018年1月18日
対角線分割法、実用化の兆し
美術講師の
湯浅さんが
びわさんのツイートを見てひらめいたんだけど、
— 湯浅誠 (@yuassamakoto) 2017年12月13日
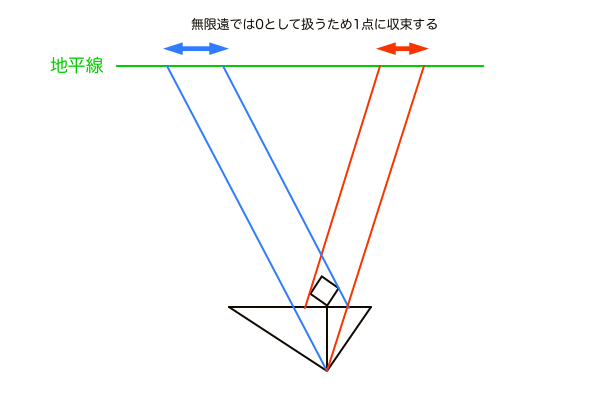
アイレベル上の画面端に向かって45°の対角線を引けば、そこが画角90°になるから、それを基準として奥行きを減らしていけば、画角の調整が可能になってくるなと。
こ、これは、すごい。
画角メーター、いらなくなるじゃん。 pic.twitter.com/h1RjWnsCvl
まず
ではどうすべきか。例えば、
出典 お絵描きホーホー論
つまり、
真理の扉の向こうにある「真・対角線分割法」
対角線分割法は、もとは
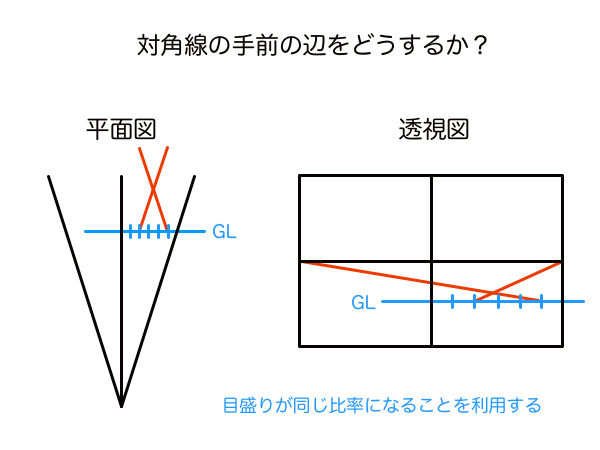
例えば、「平行な線は無限遠で同じ1点に収束する」「視界の両端と平行な線は無限遠で画面端に収束する」「PPと平行方向には奥行きの縮小は生じない」「GL幅は平面図と透視図で同一の比率で扱える」「平面図上の対角線の交点(詳細は省略)は透視図上では奥行きとなる」。これらの原理を組み合わせて作られたのが「真・対角線分割法」です。まだ試行錯誤中なので未完成ですが。透視図法の作図をしているとは思えない単純明快な手順を辿りますが、ちゃんとパースが取れる独自の手法です。ただ、透視図法を完全に理解していないとただのブラックボックス、誤用に気づけない諸刃の剣ですが。
真・対角線分割法の実演。やってて楽しいけど、これまでにないほど禍々しい作図風景になった。あとはラフレイアウトと平面図の対応のさせ方が曖昧で制度が悪くなるところを改善すれば使い物になる。 pic.twitter.com/o0pYnMxX6Q
— お絵描きホーホー論 (@oekaki_hoho_ron) 2018年1月16日