-
目次
- 1点透視図法(x,y軸=平行)
- 2点透視図法(y軸=平行)
- アイソメトリック図法(x,y,z軸=平行)
- 3点透視図法、基準はCPのみ
- なぜ4点ではなく3点なのか?
- 3つの消失点の位置を決める立方体の切断面「VP断面」
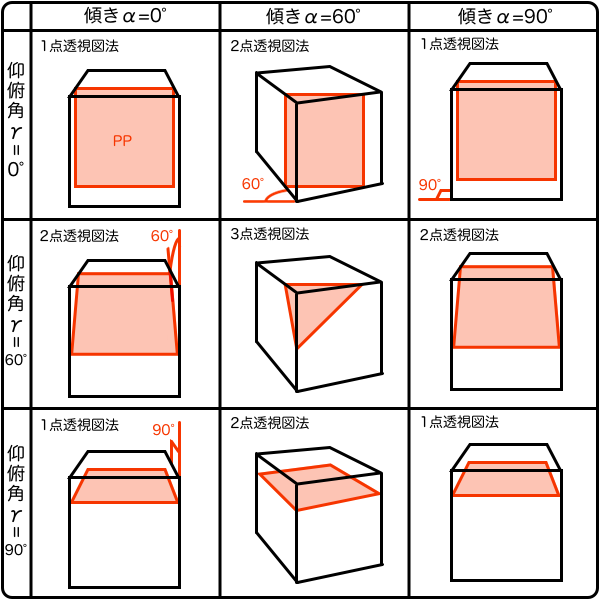
- 傾きαと仰俯角γとVP断面の形状の関係
- 3点透視図法は3つの2点透視図法という考え方
- 水平方向(SP)と垂直方向(SPV)で考えるPPの作図手順
- 透視図法の作図を極めるまであと一歩
この記事は3点透視図法を理解するために必要な情報が詰め込まれた決定版です。これまでにも3点透視図法の原理を分かりやすくまとめようと様々な考え方を提唱してきましたが、ここ最近の学びと閃きでついに3点透視図法の全貌を把握するための「3点透視図法解剖図」を完成させることができました。
透視図法を勉強するとき、1点透視図法、2点透視図法までは平面的なイメージで理解ができます。消失点とアイレベルさえ描いていれば最低限間違いをせずに作図できます。ところが3点透視図法からは消失点の位置関係がかなり複雑になります。これを理解するには3次元的なイメージが元になっていることを知っておくべきです。「3点透視図法は2点透視図法を90°回転させて垂直方向にしたもの」という説明をよく目にしますが、確かに水平方向と垂直方向にパースのかかった絵という意味では正しく思えるかもしれませんが、厳密には全く違います(具体的には後ほど)。とにかく3点透視図法の3次元的なイメージは傾きαと仰俯角γの大きさで変化するということを理解する必要があります。今回は、各種透視図法のイメージの捉えかたの違いを順を追って解説していき、そこから3点透視図法について掘り下げていきます。また、この記事は独自に提唱している「透視図法解剖図」をベースに3点透視図法を組み上げていくのでパース理論の完全形態「透視図法解剖図」の記事を理解していることを前提としています。
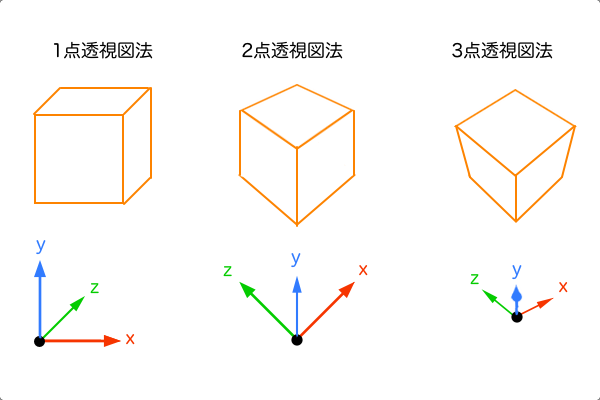
1点透視図法(x,y軸=平行)
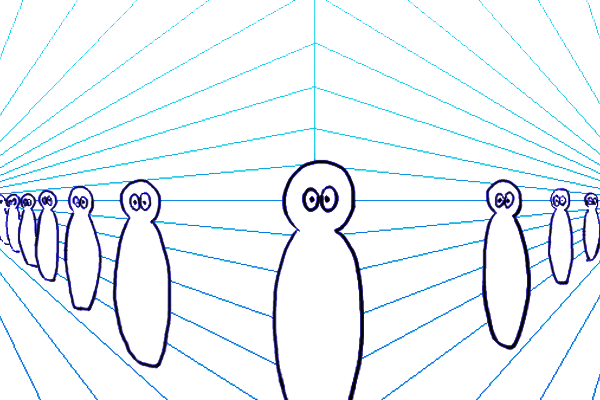
1点透視図法はVPが1つの透視図法で、奥行き方向のみに収束する見た目になります。つまり、3次元空間のxyz軸のうち2つは平面的に描かれるということです。その結果、x軸とy軸方向は 平行になり、立方体の正面が正方形に作図されます。このとき、傾きα=0°、俯角γ=0°です。
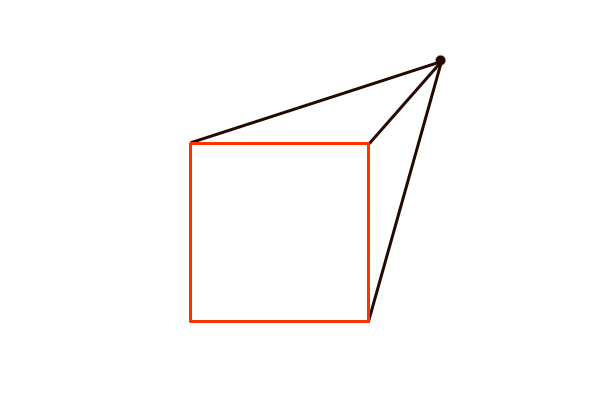
2点透視図法(y軸=平行)
2点透視図法はVPが2つの透視図法で、x軸方向の両端に奥行きが収束する見た目になります。つまり、3次元空間のxyz軸うち1つだけが平面的に描かれるということです。その結果、y軸方向は平行になり、立方体の高さ方向の全ての辺が垂直線として作図されます。このとき、傾きα=任意、俯角γ=0°です。
冒頭で触れた「3点透視図法は2点透視図法を垂直方向に回転したもの」という考え方が厳密には全くの間違いだということについて。ここで説明したように2点透視図法は垂直方向の辺は全て平行に作図されるため、たとえ2点透視図法をそっくりそのまま垂直方向に回転したところで、今度は水平方向の辺が全て平行に作図される2点透視図法になるだけです。おそらくこの解説方法を模範解答だと勘違いする人は、1点透視図法の立方体に縦パースが与えられたものを3点透視のシンプル版だと解釈していると思われますが、1点透視図法に縦パースが加わるとそれはやはり水平方向の辺が平行に作図されるだけの2点透視図法で、それこそが「2点透視図法を垂直方向に回転したもの」、これっぽっちも3点透視図法ではありません。3点透視図法はもっと複雑です。
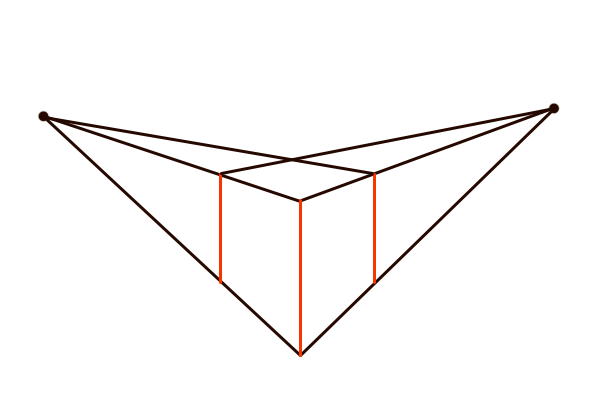
アイソメトリック図法(x,y,z軸=平行)
余談として、アイソメトリック図法はVPが存在しない抽象的な空間に立体感を表現した図法で、どの方向にも収束しない見た目になります。つまり、3次元空間のxyz軸の全てが平面的に描かれるということです。その結果、3方向に向かう線はそれぞれ平行に描かれ、立体感を表現しようとする意図は感じられますが、平面的な模様のように作図されます。ちなみに「アイソメトリック」とは「同じ長さ」という意味らしいです。
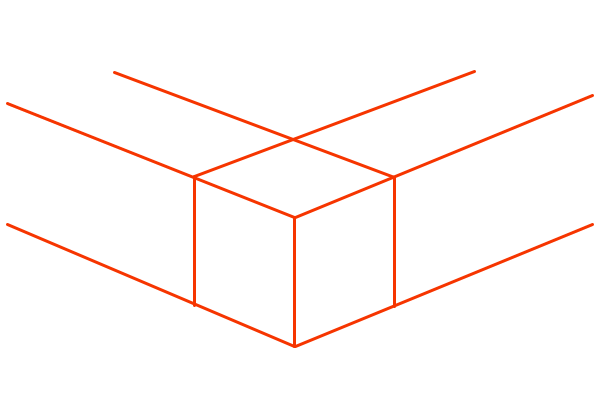
3点透視図法、基準はCPのみ
3点透視図法はVPが3つの透視図法で、3方向に収束する見た目になります。つまり、3次元空間のxyz軸のうち平面的に描かれる軸はないということです。その結果、最初の基準にできる要素はCPと一致している立方体の手前の頂点ただ一つになります。このとき、傾きα=任意、仰俯角γ=任意です。ちなみに、傾きα=0°、仰俯角γ=任意の場合は垂直方向の2点透視図法ということになり、つまり仰俯角γは垂直方向の傾きαだと考えることもできます。ちなみに、CPと一致していない点からでもそこを立方体の手前の頂点にして作図はできますが、CP以外の位置では既に奥行きの縮小がなされているため、原寸を割り出してM点法を使うことが少し手間になります。
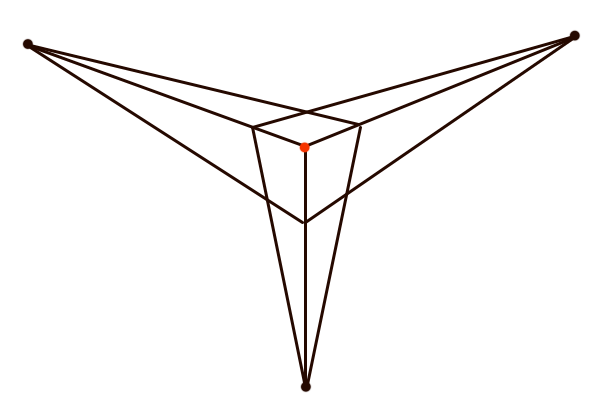
なぜ4点ではなく3点なのか?
何度も繰り返しますが、3点透視図法の解説でよく見かけるのが「2点透視図法を垂直方向にすると分かりやすい」というのは半分正解ですがもう半分は誤解を招くノイズです。2点透視図法は消失点が2つある手法なので、垂直方向にすればいいという解釈だと単純に考えて3点透視図法ではなく4点透視図法になってしまいます。4点透視図法というと魚眼パースの別名として扱われている手法で、これで作図しても3点透視図法の絵にはならないというのは試してみればすぐにわかります。
この4点目の存在が立体を余計に歪めてしまうので魚眼パースになります。まず水平方向について、2点透視図法ということは立方体には傾きαが与えられています。そして3点透視図法に発展させるには垂直方向に3つ目の消失点を設置します。しかし、ここで「3点透視図法は2点透視図法を垂直にする」という考え方を適用すると4つ目の消失点にも奥行きを収束させないといけませんが、4つ目の消失点VP4は必然的にVP3と同じ垂直線上に位置する(CP・VP3・VP4は垂直線上の位置関係)ことになり、それぞれの消失点に奥行きを収束させるには曲線で繋ぐしかなくなり、結果として魚眼パースになります。それに、4点透視図法はいわば曲線で作図した1点透視図法のことなので、VP3とVP4の垂直位置をずらすために垂直方向に傾きを与えたとしても、VP3とVP4の位置が垂直線上からずれはしますがVP3-VP4のずれに伴ってVP1-VP2も同じだけずれてしまい、結局は4点透視図法のままです。立体のアングルを変えるのではなくて、空間の歪み方自体を変えないといけません。
まずこの考え方の決定的な矛盾は、以前の透視図法の知られざる大前提 〜実は市販のパース理論書の教えは間違っていた〜の記事で提唱した2つの前提をそっくりそのまま破ってしまっているところです。前提1では「透視図法は直線で描かれる」とあるのに、VP3とVP4に収束するには曲線で収束させざるを得ないため矛盾します。前提2では「透視図法でパースの縮小が生じるのは奥行き方向のみ」とあるのに、VP3とVP4のような同じ垂直線上にある位置関係の消失点に収束するということは、奥行き方向ではなく垂直方向にパースの縮小を生じさせているため矛盾します。
出典 お絵描きホーホー論
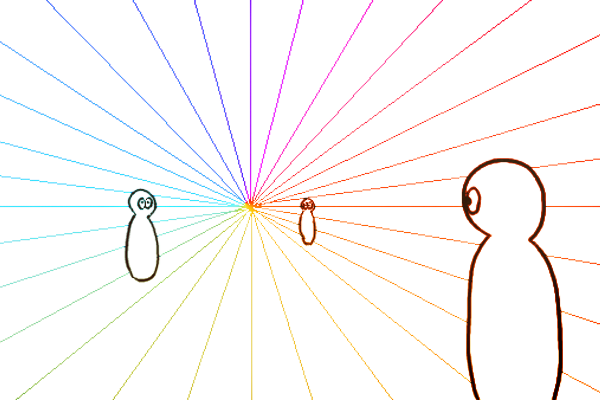
ここで、消失点の機能について改めて理解しておく必要があります。2点透視図法で使われる2つの消失点は、最終的に視円錐の底面PPに絵を作図するための基準点で、PPは円であるためタレスの法則によりSPとVP1とVP2を直線で結ぶと直角三角形となります。つまり2点透視図法で使われる対になる消失点は、SPから前方90°の範囲を挟み込むように配置されています。これによって、全ての頂点角が90°で構成される図形である「正立方体」を作図することが容易になり、単純な図形を配置することにより空間把握しやすくなります。画角が90°以外の場合でも90°を基準にして、相対的に歪みが激しいとかVP1-VP2間距離が長いという考え方で作図できます。このように、透視図法では正方形を基準にして作図するために90°もしくは対角線方向の45°を基準にして消失点が配置されています。
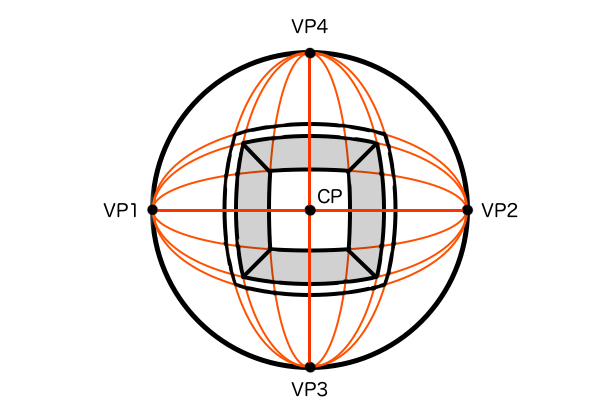
では「2点透視図法を垂直方向にして考える3点透視図法」でのVP3とVP4でも直角の位置関係になっているか検証してみましょう。まず、観察者が見ている立体は普通は地面に置かれており、垂直方向の辺はVP3に収束し、水平方向の辺はそれぞれVP1とVP2に収束します。そして、VP3と垂直線上の位置関係にあるVP4に収束するものが何かというと水平方向の面(上面・底面)ということになり、これらの面は地面と平行なのでいずれはHLに収束するため、必然的にVP4はアイレベル上に配置されます。この場合のVP4はアイレベル上にある点、すなわち立方体の水平方向の「辺」ではなく「面」が収束し、辺が収束するものではないので特定の1点は存在しないため「点」ではなく「高さ」というべきです。つまりVP4はそれ単体ではあまり意味がなく、そもそもアイレベルの機能と完全に被っており、よってVP4は必要のない点であるといえます。
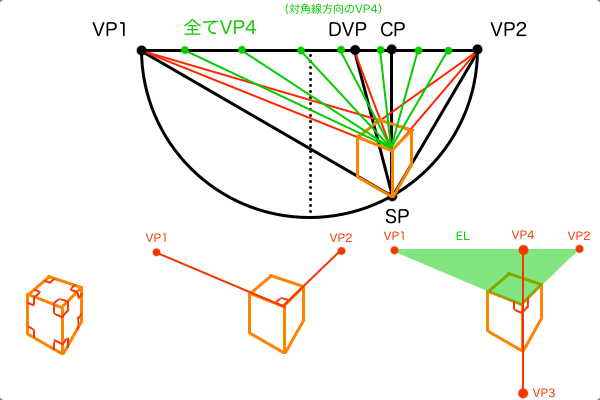
ここまでで、3次元的な透視図法で使われる消失点の数はなぜは点ではなく3点なのかを考えてきましたが、3次元というものを表現するための指標であるxyz軸(直交座標形)の形状を思い出してみれば消失点が3つであるというのが一目瞭然です。3本の直線のそれぞれが直行する位置関係で配置されると、それ以外に直行するような直線を配置する場所などなくなります。VP4というのはVP1とVP2があれば不要な点で、VP1とVP2の間に位置する消失点が必要なら対角消失点DVPというものが正式に存在します。消失点はSPから見て直角の範囲の両端に配置するということ、3次元の座標系は3本の直行する直線で構成されているということ。これらを踏まえると、3次元には直角は3つしか配置できず、その直角の範囲の両端にそれぞれ消失点を配置すると、必然的に3次元空間に消失点は3つまでしか存在できないことになります。
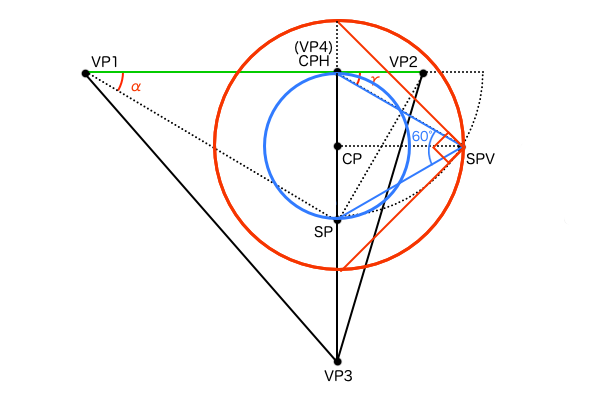
3つの消失点の位置を決める立方体の切断面「VP断面」
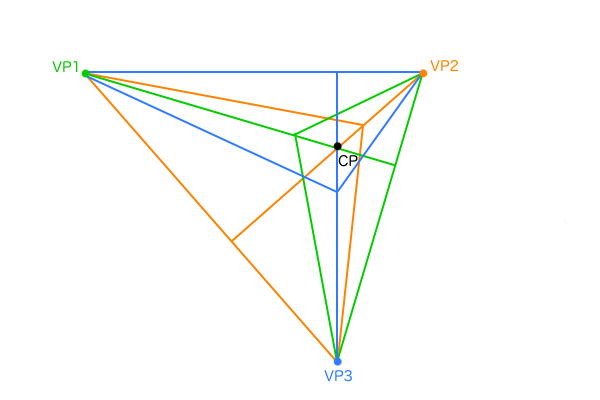
2点透視図法のVPの位置は特殊な構図でなければ常にEL上にあるため、画角θによって変化するVP1-VP2間距離Lさえ求まれば作図できました。しかし、3点透視図法はVP1、VP2、VP3を結んだ三角形の各辺がそれぞれアイレベルELとして機能しているため2点透視図法と同じようには扱えず、3次元的に考える必要があります。
3点透視図法のVPの位置は、実際に立方体の頂点を見ていると仮定して、その視線に直行するPPで立方体を切断したときの断面の三角形の各頂点として求めることができます。この断面は立方体の傾きαと、立方体を見下ろすもしくは見上げる角度の仰俯角γの大きさによって変化します。この断面は3つのVPによって作られているので、とりあえず「VP断面」と呼ぶことにします。
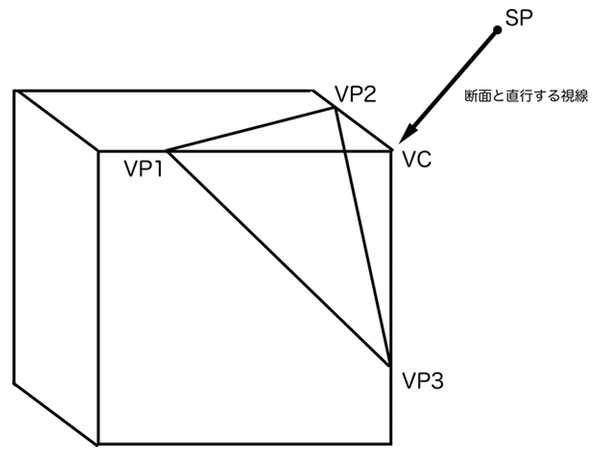
また、3点透視図法では仰俯角γというものが新たに登場します。透視図法においてVCとは観測者が注目している点ということです。3点透視図法のCPは、2点透視のときに使っていたアイレベルEL(地平線HL)から上下にずれた位置に描かれます。それが何を意味するかというと、観測者が水平方向を向いておらず、地平線HLを注目せずに見下ろし(上げ)ているということです。観測者と立体の高さ方向の位置関係は側面図を描けば一目瞭然です。そして側面図で見下ろしている角度がそのまま仰俯角γとなります。仰俯角γはVP断面の形状に関わるVP3の位置を決めるための数値なので、しっかりイメージを掴んでおきましょう。
傾きαと仰俯角γとVP断面の形状の関係
上図のVP断面の形状はだいたい傾きα45°、仰俯角γ45°くらいのものですが、それ以外の傾きαと仰俯角γがどのようにVP断面の形状に影響するかを考えるには全パターンを一覧すればイメージしやすくなります。まず、VP断面を考えるときのデフォルト状態として、傾きα=0°のときに立方体を正面から見る、仰俯角γ=0°のとき立方体を正面から見るとします。傾きα=0°では1点透視図法になり、傾きα=90°の場合も立方体の正面を同じ高さから見ているため1点透視図法となり、仰俯角γ=90°の場合も立方体を真上から見ている1点透視図法になります。要するに、何も角度が与えられていないと1点透視図法、傾きαが与えられると2点透視図法、それに仰俯角γが与えられると3点透視図法ということです。
3点透視図法は3つの2点透視図法という考え方 〜画角90°のPP作図手順〜
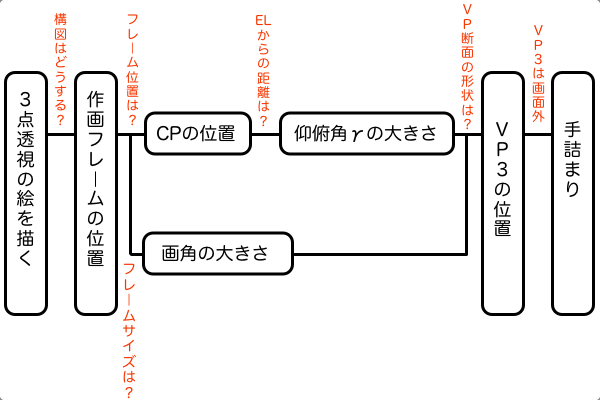
前回のパース理論の完全形態「透視図法解剖図」の記事で透視図法の全貌を掴む図として「透視図法解剖図」というものを考案しました。そして、2点透視図法と違って3点透視図法では上面、左側面、右側面に対応するSPが一つずつあるのでかなり複雑だと思っていたのですが、意外とシンプルな考え方を編み出せました。そのシンプルな考え方を透視図法解剖図に取り込むことで「3点透視図法解剖図」に進化します。それでは、まず3点透視図法のPPの考え方について解説しておきます。
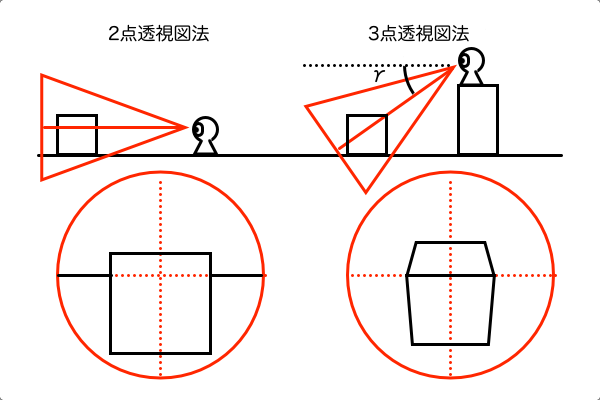
3点透視図法で思い通りの絵を描くためには透視図法解剖図の中に正しい大きさの作画フレームを正しく配置しないといけません。そして作画フレームの位置はCPの位置によって決まり、作画フレームのサイズは画角の大きさによって決まります。しかし、3点透視図法は見上げたり見下ろした構図の絵なのでCPはアイレベルの高さ以外に移動しており、さらに縦パースが加わることにより画角の求め方も少し変わってきます。それらCPの位置や画角の大きさを決めるためには仰俯角γやVP断面を作図する必要があり、そのためにはVP3の位置を把握できてないといけません。しかし、大抵の場合VP3はアイレベルの遥か下の方に位置するため紙の上で作図するのは不可能です。
2点透視図法における画角90°の視円錐の作図のときは、VP1-VP2間距離を直径とする円を描けば済みましたが、それは地面と視線が平行の場合すなわち仰俯角γが与えられていない場合のみの考え方です。仰俯角γが与えられた3点透視図法では地面と視線が平行でないため、立方体の全ての辺が奥行き方向に少しずつ傾斜した状態となります。それは言い換えると、VP断面の三角形の各辺をそれぞれアイレベルとして見る2点透視図法が3つあるということになります。ここで、3つの2点透視図法の個々のVP-VP距離に注目してみると、VP断面の形状によっては長さがバラバラとなりPP直径もバラバラ、それは2点透視図法のときと同じ考え方を適用すると画角もバラバラということになります。
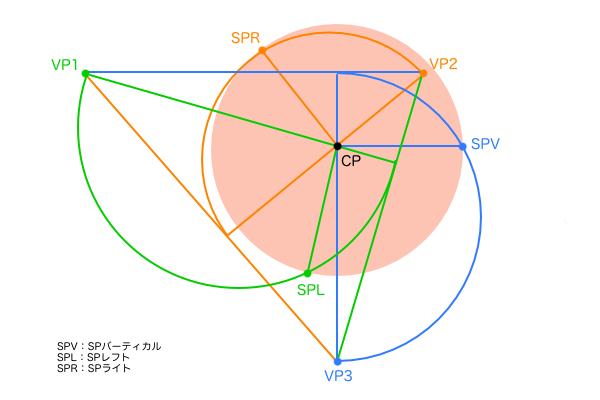
そこで、3つの2点透視図法の画角を統一するために公約数的なPPを作図しようとすると、今度は3つの2点透視図法のSPに注目する必要があります。面白いことに、3つの2点透視図法のPP直径はバラバラですが、PP-SP距離は見事に一致します。あとはCPを中心点とする3つのSPを円周上にもつ円を作図すれば、それが画角90°のPPとなります。
ただ、既に述べたようにこの方法では紙の上だけで話が完結しません。この方法は、立方体の上面、右側面、左側面に対応する2点透視図法を利用するものですが、それだと必ずVP3の位置を把握できてないといけないのでアナログには不向きです。そうなると手詰まりとなるのですが、3点透視図法の原理をうまく利用することで極力作画フレームに近い位置でCPと画角90°の視円錐を作図できます。
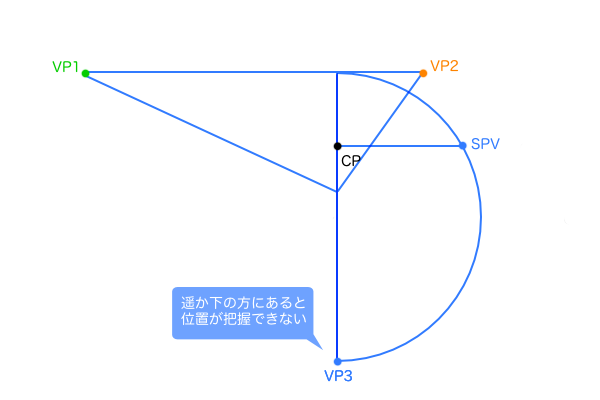
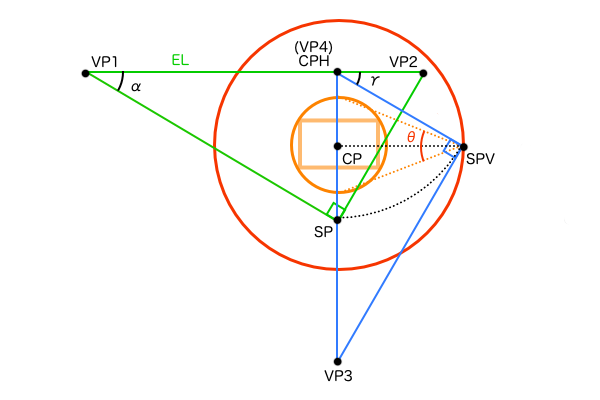
水平方向(SP)と垂直方向(SPV)で考えるシンプルなPPの作図手順
その2つの次元というのは「水平方向」と「垂直方向」のことです。3次元の「x、y、z軸」でもなく、立方体の「上面、左側面、右側面」でもなく、観測者基準の「縦と横」だけです。では、具体的に何に対して水平、垂直なのかというと観測者の視界に対してです。つまり、3点透視図法の画角90°の視円錐を作図するために使う2つの次元の視円錐とは、視界の視円錐における水平方向または垂直方向の視円錐のことになります。立方体基準にしていた場合のxyz軸だと立体の傾きαや仰俯角γによって軸の角度が変わってしまい、それをSPから見たときの立方体の各面の奥行きの圧縮具合も複雑に変わってしまいます。観測者の視線を基準にすれば軸の角度はPPの中央の十文字と一致するので常に一定で、水平方向、垂直方向、奥行き方向で3次元を表現できます。
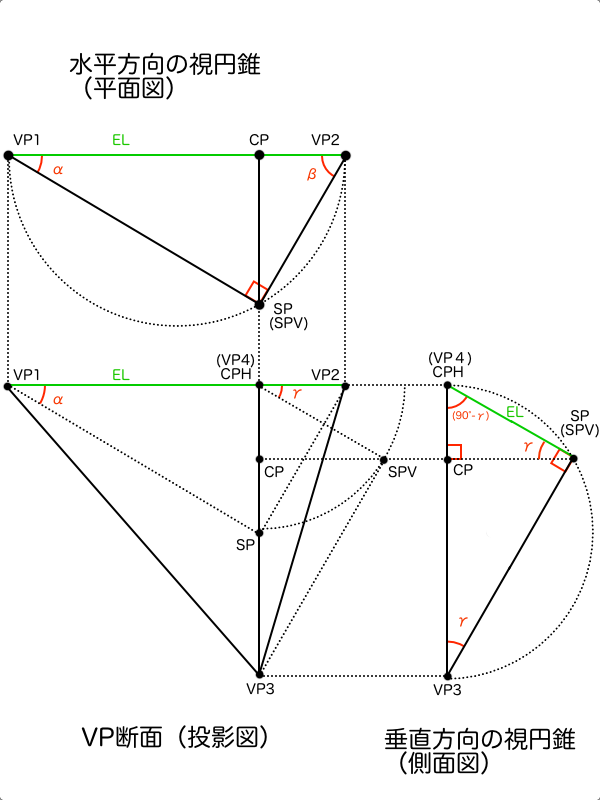
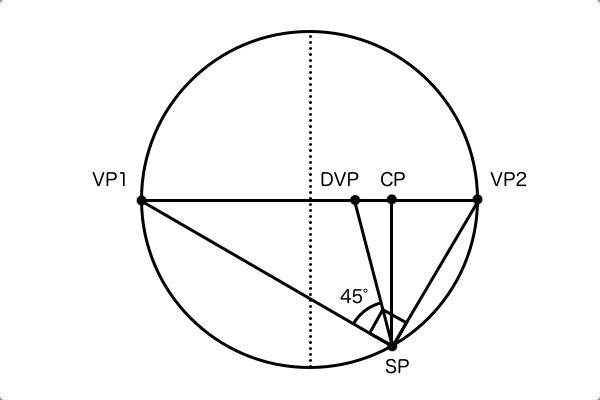
そしてこの2つの視円錐を使う最大のメリットは、それぞれの視円錐のなかで同じ寸法の辺が存在しているため対応させやすいということです。その同じ寸法の辺というのは下図のオレンジで描かれている辺です。それぞれ水平方向と垂直方向の視円錐の中で地面に平行な線として作図されているため、3次元空間で捉えれば同じ線となります。そして、これを3点透視図法の解剖図で見ると、お互いが同じ点を始点とし、尚且つ同じ寸法の線分であるため、つまり2つの線分の終点側は同じ円弧上に存在するということになります。よって水平方向の視円錐でCPを中心点としCPH-SP間距離を直径とする円を描けば、垂直方向の視円錐のSPVの位置がかなり絞れます。
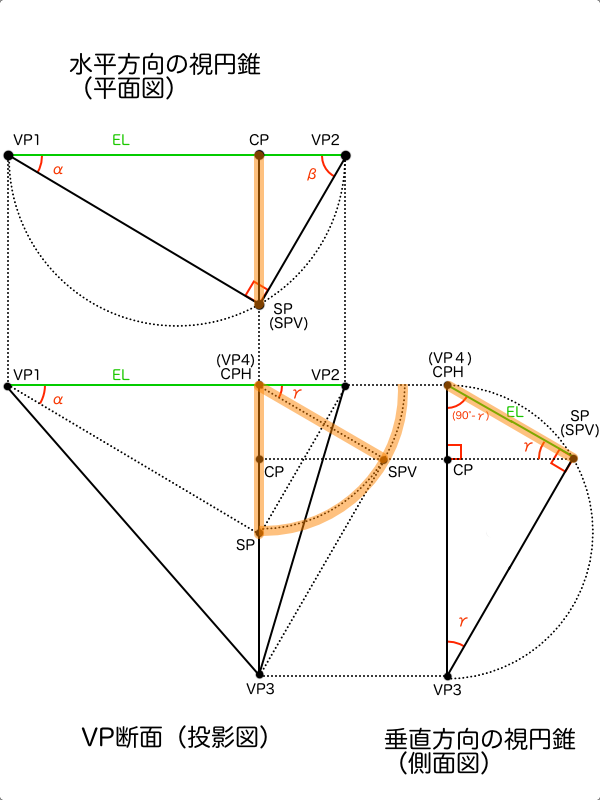
さらに、側面図の直角三角形を見ると△SPV-VP3-CPHと△SPV-CP-CPHは相似の関係であることが分かり、仰俯角γを設定した場合のSPVは、∠VP2-CPH-SPVが(90°-γ)の方向の円弧上にあると特定できます。そしてSPVを通る水平線とSPを通る垂直線の交点が視心CPとして求まります。
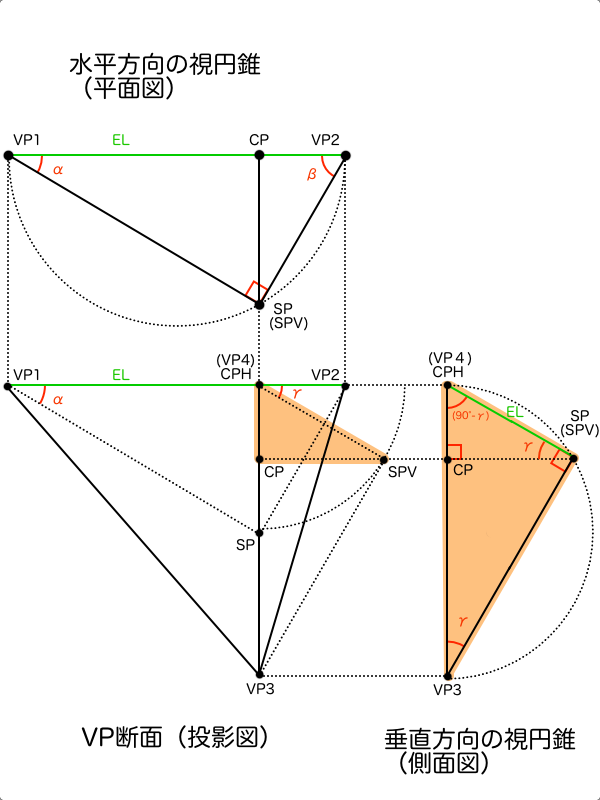
CPの位置が確定したので作画フレームの位置は作図できるようになりました。あとは作画フレームのサイズを確定するために、まずは画角90°の視円錐を作図する必要があります。画角90°の視円錐はCPを中心とするSPを円周上に持つ円なので、その通りにCPを中心とするSPVを通る円を描きます。画角θが小さい場合の視円錐を描くなら、SPVからCPを見ているとき任意の画角θの範囲になる円を描くだけです。ただ、画角が90°未満のときに紙に絵を描くとした場合、画角90°の視円錐は画面外にあるためSPVの位置を把握できません。そのときは2点透視図法と同じ様に水平方向の画面幅を使って、任意の画角θの視円錐のSPから何度の方向(ex 画角30°ならSP角150°)にVPがある、と考えれば問題ありません。しかしながら、この方法では紙の上の遥か外側にVPがある望遠パースのときにアナログで正確に作図できないのは2点透視図法のときと同じですね。
透視図法の作図を極めるまであと一歩
そしてこちらが完成した3点透視図法解剖図です。
1点、2点、3点の透視図法解剖図を理解できれば透視図法の「作図」に関する基礎知識は網羅できているはずです。ただ一つ、まだ3点透視図法における奥行きの長さの作図手順は解説していません。次の記事では奥行きの長さの作図のみを徹底的に掘り下げるつもりですが、一般的な奥行きの長さを作図する手法であるD点法やM点法ではなく、もっと便利な手法を開発しようと思います。M点法の上位互換になる奥行きを比率で分割するR点法です。